All right, now I got your question – rather, questions. Who’s Mr Venn? Why would he come to teach English? What is he teaching now? Before you inundate me with all those questions, let me tell you about him.

John Venn, FRS, FSA (4 August 1834 – 4 April 1923) was an English logician and philosopher noted for introducing the Venn diagram, used in the fields of set theory, probability, logic, statistics, and computer science
John Venn – Wikipedia
That was the first few lines, lazily quoted from Wikipedia, where you can learn more about him. Okay, he brought in Venn diagrams, so what?
Understanding set language became better. People were able to “see” sets as physical objects. They were able to easily prove various properties of set operations – one of the basics being defining a subset.
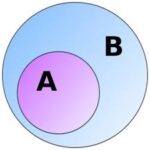
Set A is said to be a subset of B (the superset) if all elements of A are also elements of B. This is checking that every element of A is an element of B. However, with a Venn diagram, this became uber-cool (see Figure 1).
[Okay, there is also the possibility of a subset being identical to the superset; we call the former an improper subset. By the way, whenever we talk about a set, the universal set comes into existence, often without express request. If you draw only one circle on a piece of paper to represent a set, say, of even numbers, then the universal set is the white space around the set (the set of all natural numbers). Universal set is all inclusive. It’s like Lord Krishna’s wide open mouth, where you can see everything in the universe.]
Now that you have a set, rather a universal set, define a criterion and you have shelved out a subset.
Come again.
Define a criterion and you have shelved out a proper subset.
You have divided the original set into two: the have and the have-not! I mean, the one that “has that quality” and the other that “does not have the quality”.
This criterion, in English, is called relative clauses – to be accurate, restrictive relative clauses.
Relative clauses are clauses that begin with a relative pronoun (such as who, that, where, and when) and define a noun.
By defining a criterion, we define restrictive, or defining, relative clauses.
You can easily see that restrictive relative clauses create a proper subset of the noun clauses.
Let’s see an example.
The work–life balance of the employees surveyed is significantly higher in organizations that follow the 5-day work week.
Mathematically, the clause “that follow the 5-day workweek” is a defining criterion for the subset.
Looking through the grammar lens, it is a relative clause because it begins with “that”, a relative pronoun.
With the risk of being redundant, defining a proper subset is nothing but writing down a restrictive (defining) relative clause. Understanding one helps us understand the other.
Also noteworthy is the fact that these restrictive relative clauses create a proper subset. So, aren’t there restrictive relative clauses that create an improper subset of a set. In other words, can we write down a criterion that will not create a proper subset, but becomes the same as the original set?
In other other words, when there is something called restrictive relative clauses, are there non-restrictive relative clauses?
The answer is we can and there are.
To know more, I’m going to request you to wait until the next post.
Meanwhile, if you love math, practise restrictive relative clauses with the help of Mr. Venn; if you love English, get to know Mr. Venn through grammar.




0 Comments